Nghiên cứu đột phá về phương pháp tối ưu hóa hiệu suất LLM với Adaptive Generation và Weighted Ensemble
📝 Tóm Tắt
Chúng tôi nghiên cứu phương pháp Best-of-N cho các mô hình ngôn ngữ lớn (LLMs) với việc lựa chọn dựa trên bỏ phiếu đa số.
Đặc biệt, chúng tôi phân tích giới hạn khi N tiến đến vô cùng, mà chúng tôi gọi là Best-of-∞.
Mặc dù phương pháp này đạt được hiệu suất ấn tượng trong giới hạn, nó đòi hỏi thời gian tính toán vô hạn.
Để giải quyết vấn đề này, chúng tôi đề xuất một sơ đồ sinh câu trả lời thích ứng chọn số lượng N dựa trên sự đồng thuận của câu trả lời,
từ đó phân bổ hiệu quả tài nguyên tính toán. Ngoài tính thích ứng, chúng tôi mở rộng khung làm việc đến các
tổ hợp có trọng số của nhiều LLMs, cho thấy rằng các hỗn hợp như vậy có thể vượt trội hơn bất kỳ mô hình đơn lẻ nào.
Trọng số tổ hợp tối ưu được xây dựng và tính toán hiệu quả như một bài toán lập trình tuyến tính hỗn hợp nguyên.
🚀 Giới Thiệu
Trong những năm gần đây, chúng ta đã chứng kiến những tiến bộ đáng kể trong lĩnh vực Large Language Models (LLMs),
từ các mô hình đóng như Gemini, GPT, Claude đến các mô hình mã nguồn mở như Llama, DeepSeek, Qwen.
Một trong những mối quan tâm lớn nhất trong lĩnh vực LLMs là khả năng thực hiện các nhiệm vụ suy luận phức tạp.
Việc sử dụng nhiều tài nguyên tính toán hơn tại thời điểm kiểm tra, đặc biệt bằng cách tạo ra nhiều câu trả lời,
dẫn đến suy luận đáng tin cậy hơn. Một chiến lược đơn giản nhưng hiệu quả là phương pháp Best-of-N (BoN),
nơi chúng ta tạo ra N câu trả lời và chọn câu trả lời tốt nhất dựa trên một số tiêu chí.
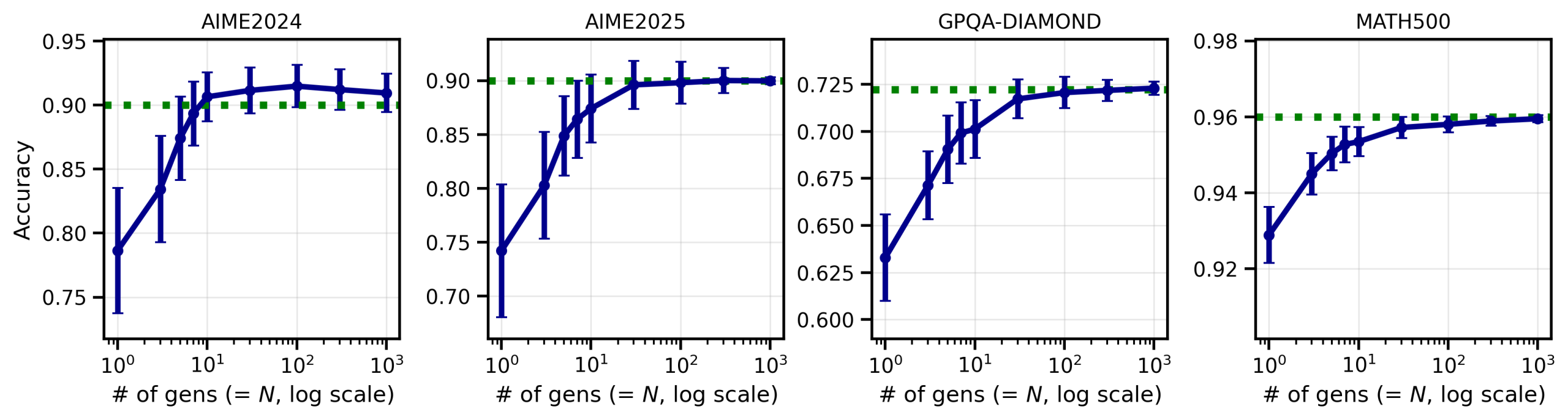
Hình 1: Độ chính xác của Best-of-N với bỏ phiếu đa số theo hàm của N (GPT-OSS-20B) với bốn datasets.
Đường màu xanh lá chỉ ra độ chính xác tiệm cận của N→∞.
Có nhiều cách để triển khai chiến lược BoN. Một cách tiếp cận phổ biến là sử dụng reward model để chọn câu trả lời tốt nhất
hoặc yêu cầu LLM chọn câu trả lời ưa thích. Một cách tiếp cận khác là bỏ phiếu đa số trong đó câu trả lời xuất hiện
thường xuyên nhất được chọn.
Mặc dù đơn giản, bỏ phiếu đa số có nhiều ưu điểm. Đầu tiên, nó không yêu cầu mô hình hóa bổ sung hoặc tạo văn bản thêm.
Thứ hai, so với các phương pháp khác, bỏ phiếu đa số có khả năng chống lại reward hacking và hưởng lợi từ việc tạo thêm với rủi ro tối thiểu,
không giống như các mô hình dựa trên reward nơi việc tăng N có thể dẫn đến overfitting.
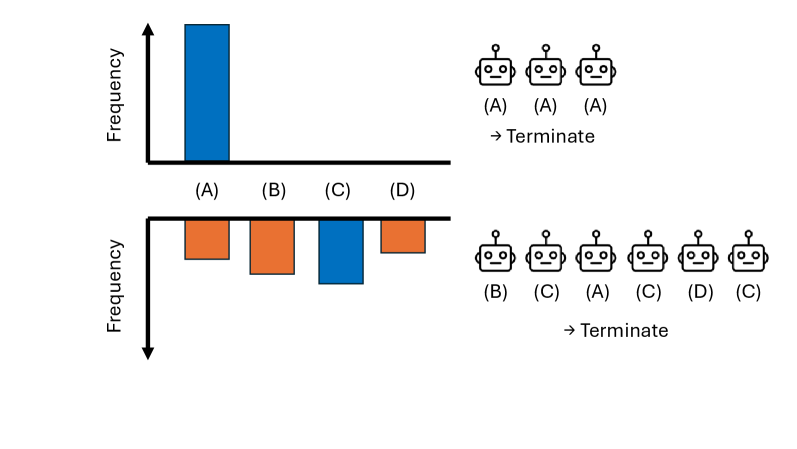
Hình 2: Minh họa adaptive sampling (Algorithm 1). Histogram cho thấy phân phối các câu trả lời được tạo bởi LLM cho một bài toán đơn lẻ.
Màu xanh dương chỉ ra câu trả lời xuất hiện nhiều nhất, màu cam chỉ ra các câu trả lời khác.
Mặc dù chúng ta mong muốn đạt được hiệu suất Best-of-N như vậy khi N→∞, mà chúng ta gọi là hiệu suất Best-of-∞,
nó đòi hỏi một số lượng vô hạn các thế hệ (mẫu), điều này không khả thi trong các tình huống thực tế.
Tuy nhiên, với cùng ngân sách thời gian kiểm tra, chúng ta có thể sử dụng ngân sách có sẵn hiệu quả hơn.
Như được thể hiện trong Hình 2, chúng ta có thể tạo mẫu một cách thích ứng cho đến khi chúng ta xác định được đa số với một mức độ tin cậy nào đó.
Sơ đồ của chúng tôi có thể được mở rộng tự nhiên đến các tổ hợp của nhiều LLMs. Quan trọng là, bỏ phiếu đa số tổ hợp có thể tự nhiên
hưởng lợi từ tính bổ sung. Ví dụ, trong dataset AIME2025, hiệu suất Best-of-∞ của GPT-OSS-20B và Nemotron-Nano-9B-v2 lần lượt là 90.0% và 73.0%,
nhưng tổ hợp của chúng đạt được 93.3%. Một LLM yếu có thể đóng góp vào tổ hợp nếu nó có điểm mạnh bổ sung.
♾️ Best-of-∞ trong Mẫu Hữu Hạn
Trong khi Best-of-∞ định nghĩa một tổ hợp Best-of-N lý tưởng trong giới hạn N→∞, việc thực hiện theo nghĩa đen sẽ đòi hỏi
tính toán thời gian kiểm tra không giới hạn. Bây giờ chúng tôi phát triển một quy trình mẫu hữu hạn theo dõi chặt chẽ giới hạn này.
Ý tưởng cốt lõi của chúng tôi là lấy mẫu thích ứng (tức là yêu cầu LLM tạo ra câu trả lời) cho đến khi chúng ta chắc chắn
về bỏ phiếu đa số dân số với mức độ tin cậy mong muốn. Nói cách khác, chúng ta nhằm mục đích kết thúc quá trình tạo câu trả lời
ngay khi có đủ bằng chứng thống kê để hỗ trợ kết luận rằng phản hồi hiện tại xuất hiện thường xuyên nhất tương ứng với đa số thực sự,
điều này cho phép số lượng N khác nhau trên các vấn đề.
Một thách thức đặc biệt của vấn đề này nằm ở thực tế là hỗ trợ của phân phối câu trả lời được tạo bởi các mô hình ngôn ngữ lớn (LLMs)
là không xác định. Ví dụ, trong một trường hợp, LLM có thể tạo ra hai câu trả lời ứng viên, chẳng hạn như 42 với xác suất 70% và 105 với xác suất 30%,
trong khi trong trường hợp khác, nó có thể tạo ra bốn đầu ra riêng biệt, chẳng hạn như 111 với xác suất 40%, 1 với xác suất 25%,
2 với xác suất 20%, và 702 với xác suất 15%.
Với sự không chắc chắn như vậy trong sự thay đổi của các phản hồi được tạo, một cách tiếp cận đặc biệt phù hợp là sử dụng
mô hình hóa Bayesian không tham số. Đặc biệt, chúng tôi áp dụng một quy trình Dirichlet DP(H,α) trước trên không gian câu trả lời
nắm bắt phân phối không xác định của các câu trả lời. Ở đây, H là phân phối cơ sở trên không gian câu trả lời, và α > 0 là tham số tập trung
kiểm soát khả năng tạo ra câu trả lời mới.
🔧 Algorithm 1: Approximated Best-of-∞
Chúng tôi sử dụng Bayes factor để đo lường bằng chứng của đa số thực sự. Chính thức, chúng tôi định nghĩa các giả thuyết như sau:
📊 Định Nghĩa Giả Thuyết
H₀: Câu trả lời xuất hiện thường xuyên nhất A₁ không phải là đa số thực sự.
H₁: Câu trả lời xuất hiện thường xuyên nhất A₁ là đa số thực sự.
Bayes Factor: BF = P(D(n)|H₁) / P(D(n)|H₀)
Khi n đủ lớn so với α, P(H₁|D(n)) của posterior DP có thể được xấp xỉ bằng phân phối Dirichlet.
Mặc dù số lượng này không dễ tính toán, nó có thể được ước tính bằng các phương pháp Monte Carlo bằng cách lấy mẫu từ phân phối Dirichlet.
🎯 Định Lý 1: Sự Hội Tụ
Nếu chúng ta đặt N_max và B đủ lớn, hiệu suất của thuật toán hội tụ đến hiệu suất Best-of-∞.
Điều này đảm bảo rằng phương pháp adaptive sampling của chúng ta có thể đạt được hiệu suất gần như tối ưu
với số lượng mẫu hữu hạn.
🤝 Tổ Hợp LLM
🎯 Best-of-One
Trong phần này, chúng tôi mở rộng khung làm việc Best-of-∞ đến các tổ hợp có trọng số của nhiều LLMs.
Giả sử chúng ta có K LLMs khác nhau, mỗi LLM có thể tạo ra các câu trả lời khác nhau cho cùng một câu hỏi.
Mục tiêu của chúng ta là tìm ra cách kết hợp các LLMs này để đạt được hiệu suất tối ưu.
♾️ Best-of-∞
Câu hỏi trung tâm của chúng ta là làm thế nào để chọn một vector trọng số w tối đa hóa độ chính xác f(w).
Lemma sau đây ngụ ý độ khó của việc tối ưu hóa f(w).
📝 Lemma 2: Non-concavity
f(w) là một hàm không lồi trên không gian simplex của w. Điều này có nghĩa là các phương pháp dựa trên gradient
sẽ không thể tìm ra giải pháp tối ưu toàn cục.
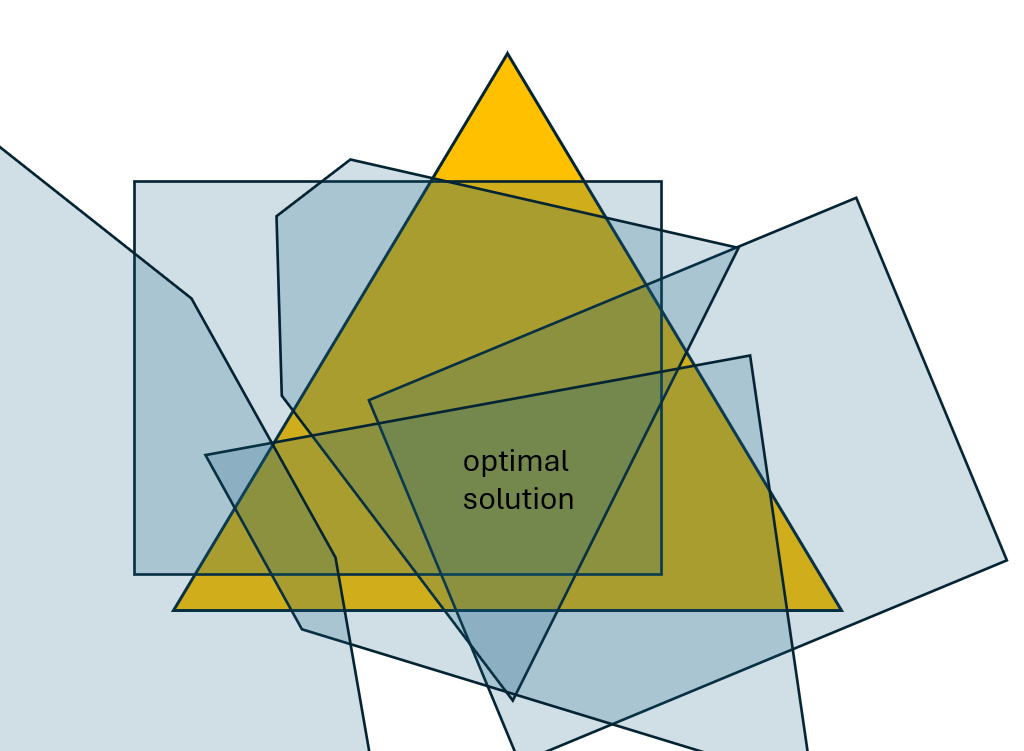
Hình 3: Visualization của hàm mục tiêu không lồi f(w) trên weight simplex w.
Simplex màu vàng tương ứng với w trong simplex của các trọng số của ba LLMs.
Mặc dù non-concavity ngụ ý tính tối ưu dưới của các phương pháp dựa trên gradient, một cách tiếp cận tối ưu hóa tổ hợp
có thể được áp dụng cho các trường hợp có quy mô điển hình. Điểm mấu chốt trong việc tối ưu hóa f(w) là tổng trong phương trình
nhận giá trị một trong một polytope.
📝 Lemma 3: Polytope Lemma
Cho {p^q_ij} là các phân phối tùy ý của các câu trả lời. Khi đó, tập hợp sau, ngụ ý rằng câu trả lời j là câu trả lời
xuất hiện thường xuyên nhất, là một polytope: {w ∈ Δ_K : Σ_i w_i p^q_ij > max_{j’≠j} Σ_i w_i p^q_ij’}
Lemma 3 nói rằng việc tối đa hóa số lượng câu trả lời đúng tương đương với việc tối đa hóa số lượng polytopes chứa w.
Bằng cách giới thiệu biến phụ y_q chỉ ra tính đúng đắn cho mỗi câu trả lời, điều này có thể được xây dựng như một
bài toán lập trình tuyến tính hỗn hợp nguyên (MILP).
📝 Lemma 4: MILP Formulation
Việc tối đa hóa f(w) tương đương với bài toán MILP sau:
max Σ_q y_q
s.t. w_i ≥ 0 ∀_i, Σ_i w_i = 1, A_q w ≥ -m(1-y_q) ∀q
trong đó A_q là ma trận kích thước ℝ^{|𝒜_q|×K}
⚖️ Max Margin Solutions
Như chúng tôi đã minh họa trong Hình 3, hàm mục tiêu f(w) có vùng liên tục của các giải pháp tối ưu.
Trong khi bất kỳ điểm nội thất nào trên vị trí này đều tối ưu trong Best-of-∞, hiệu suất hữu hạn-N của nó có thể thay đổi.
Trong bài báo này, chúng tôi áp dụng giải pháp “max margin”, tức là ở phần nội thất nhất của giải pháp.
Cụ thể, chúng tôi giới thiệu margin ξ > 0 và thay thế A_q w trong phương trình với A_q w – ξ.
Chúng tôi chọn supremum của margin ξ sao cho giá trị mục tiêu Σ_q y_q không giảm, và áp dụng giải pháp trên margin như vậy.
🧪 Thí Nghiệm
Phần này báo cáo kết quả thí nghiệm của chúng tôi. Chúng tôi xem xét các nhiệm vụ suy luận nặng trên các LLMs mã nguồn mở
mà chúng tôi có thể kiểm tra trong môi trường cục bộ của mình. Chúng tôi đặt siêu tham số α = 0.3 của Algorithm 1 cho tất cả các thí nghiệm.
Để giải MILPs, chúng tôi sử dụng highspy, một giao diện Python mã nguồn mở cho bộ tối ưu hóa HiGHS,
cung cấp các solver tiên tiến cho LP, MIP và MILP quy mô lớn. Chúng tôi áp dụng giải pháp max-margin được mô tả trong Phần 3.2.
Trừ khi được chỉ định khác, tất cả kết quả được ước tính từ 100 lần chạy độc lập. Bayes factor được tính toán với 1,000 mẫu Monte Carlo từ posterior.
📊 LLMs và Datasets Được Test
Chúng tôi đánh giá các LLMs mã nguồn mở (≤ 32B tham số) trên bốn benchmark suy luận. Chúng tôi sử dụng các bộ vấn đề sau:
AIME2024, AIME2025, GPQA-DIAMOND (Graduate-Level Google-Proof Q&A Benchmark), và MATH500.
Các datasets này là các nhiệm vụ suy luận toán học và khoa học đầy thách thức.
📈 Large-scale Generation Dataset
Chúng tôi tạo ra một tập hợp các câu trả lời ứng viên bằng cách truy vấn LLM với câu lệnh vấn đề.
Cho mỗi cặp (LLM, vấn đề), chúng tôi tạo ra ít nhất 80 câu trả lời—một bậc độ lớn lớn hơn 8 thế hệ điển hình
được báo cáo trong hầu hết các báo cáo kỹ thuật LLM. Chúng tôi tin rằng độ khó của các vấn đề cũng như quy mô
của các token được tạo ra đáng kể lớn hơn công việc hiện có về tính toán thời gian kiểm tra.
📊 Thống Kê Dataset
📊 Kết Quả Thí Nghiệm
🎯 Experimental Set 1: Hiệu Quả của Adaptive Sampling
Trong thí nghiệm đầu tiên, chúng tôi so sánh hiệu quả của phương pháp adaptive sampling với phương pháp fixed BoN.
Kết quả cho thấy rằng Algorithm 1 với kích thước mẫu trung bình N̄=3 đạt được độ chính xác tương tự như fixed sample của N=10,
cho thấy hiệu quả đáng kể của adaptive sampling.
🤝 Experimental Set 2: Ưu Thế của LLM Ensemble
Thí nghiệm thứ hai chứng minh ưu thế của tổ hợp LLM so với mô hình đơn lẻ. Chúng tôi kết hợp năm LLMs:
EXAONE-Deep-32B, MetaStone-S1-32B, Phi-4-reasoning, Qwen3-30B-A3B-Thinking, và GPT-OSS-20B trên GPQA-Diamond.
Trọng số được tối ưu hóa thành w=(0.0176,0.0346,0.2690,0.4145,0.2644). Tổ hợp LLM vượt trội hơn bất kỳ mô hình đơn lẻ nào với N≥5.
⚖️ Experimental Set 3: Học Trọng Số Tốt
Thí nghiệm thứ ba khám phá việc học trọng số tối ưu từ dữ liệu. Chúng tôi sử dụng số lượng mẫu khác nhau để xác định trọng số
và đo hiệu suất Best-of-∞ trên AIME2025. Kết quả cho thấy rằng chỉ cần một số lượng mẫu tương đối nhỏ là đủ để học được trọng số tốt.
🔄 Experimental Set 4: Transfer Learning của Trọng Số Tối Ưu
Thí nghiệm thứ tư khám phá khả năng transfer learning của trọng số được học từ một dataset sang dataset khác.
Kết quả cho thấy rằng trọng số được học từ một dataset có thể được áp dụng hiệu quả cho các dataset khác,
cho thấy tính tổng quát của phương pháp.
📊 Experimental Set 5: So Sánh với Các Phương Pháp Chọn Câu Trả Lời Khác
Thí nghiệm cuối cùng so sánh phương pháp của chúng tôi với các phương pháp chọn câu trả lời khác, bao gồm LLM-as-a-judge,
reward models, và self-certainty. Kết quả cho thấy Majority Voting đạt hiệu suất cao thứ hai sau Omniscient,
vượt trội hơn các phương pháp khác.
📈 Kết Quả Hiệu Suất Chi Tiết
Kết quả cho thấy Majority Voting đạt hiệu suất cao thứ hai sau Omniscient,
vượt trội hơn các phương pháp dựa trên reward model và LLM-as-a-judge. Điều này chứng minh tính hiệu quả
của phương pháp đơn giản nhưng mạnh mẽ này.
🔍 Phát Hiện Chính
✅ Hiệu Quả Adaptive Sampling
Phương pháp adaptive sampling giảm đáng kể số lượng thế hệ cần thiết
trong khi vẫn duy trì hiệu suất cao. Algorithm 1 với N̄=3 đạt được
độ chính xác tương tự như fixed sample của N=10, cho thấy hiệu quả
tính toán đáng kể.
🤝 Ưu Thế Ensemble
Tổ hợp có trọng số của nhiều LLMs vượt trội hơn bất kỳ mô hình đơn lẻ nào,
đặc biệt khi có tính bổ sung. Ensemble đạt 93.3% so với 90.0% của mô hình tốt nhất,
chứng minh giá trị của việc kết hợp các mô hình.
⚖️ Tối Ưu Hóa Trọng Số
Việc tối ưu hóa trọng số ensemble được giải quyết hiệu quả
như một bài toán MILP, cho phép tìm ra trọng số tối ưu một cách có hệ thống.
Phương pháp max-margin đảm bảo tính ổn định cho các ứng dụng thực tế.
📊 Quy Mô Lớn
Thí nghiệm với 11 LLMs và 4 datasets, tổng cộng hơn 3,500 thế hệ
cho mỗi kết hợp LLM–dataset, đại diện cho quy mô lớn nhất trong nghiên cứu hiện tại.
Dataset này sẽ được phát hành cho nghiên cứu tiếp theo.
💡 Insights Quan Trọng
- Bayes Factor hiệu quả: Phương pháp Bayes Factor cho phép dừng adaptive sampling một cách thông minh,
tiết kiệm tài nguyên tính toán đáng kể. - Tính bổ sung của LLMs: Các LLMs yếu có thể đóng góp tích cực vào ensemble nếu chúng có điểm mạnh bổ sung.
- Transfer learning: Trọng số được học từ một dataset có thể được áp dụng hiệu quả cho các dataset khác.
- Robustness: Majority voting robust hơn các phương pháp dựa trên reward model và ít bị ảnh hưởng bởi reward hacking.
🎯 Kết Luận
Trong bài báo này, chúng tôi xem chiến lược Best-of-N với bỏ phiếu đa số như việc lấy mẫu từ
phân phối câu trả lời cơ bản, với hiệu suất Best-of-∞ được định nghĩa tự nhiên.
Để xấp xỉ giới hạn này với một số lượng hữu hạn các mẫu, chúng tôi giới thiệu một phương pháp lấy mẫu thích ứng dựa trên Bayes Factor.
Chúng tôi cũng nghiên cứu vấn đề tổng hợp phản hồi từ nhiều LLMs và đề xuất một bỏ phiếu đa số
tận dụng hiệu quả điểm mạnh của các mô hình cá nhân. Hiệu suất Best-of-∞ có ưu thế vì trọng số của
tổ hợp LLM có thể được tối ưu hóa bằng cách giải một bài toán lập trình tuyến tính hỗn hợp nguyên.
Các thí nghiệm rộng rãi của chúng tôi chứng minh hiệu quả của phương pháp được đề xuất.
Chúng tôi đã thử nghiệm với 11 LLMs được điều chỉnh theo hướng dẫn và bốn bộ vấn đề suy luận nặng,
với ít nhất 80 thế hệ cho mỗi kết hợp LLM–bộ vấn đề. Điều này đại diện cho quy mô lớn hơn đáng kể
của tính toán thời gian kiểm tra so với công việc trước đây.
🚀 Tác Động và Ý Nghĩa
Nghiên cứu này mở ra những khả năng mới trong việc tối ưu hóa hiệu suất LLM thông qua
adaptive generation và weighted ensemble, đặc biệt quan trọng cho các ứng dụng yêu cầu độ chính xác cao
như toán học, khoa học và suy luận phức tạp. Phương pháp này có thể được áp dụng rộng rãi
trong các hệ thống AI thực tế để cải thiện độ tin cậy và hiệu suất. Việc phát hành dataset
và source code sẽ thúc đẩy nghiên cứu tiếp theo trong lĩnh vực này.
⚠️ Hạn Chế và Hướng Phát Triển
Mặc dù có những kết quả tích cực, nghiên cứu này vẫn có một số hạn chế. Việc tối ưu hóa MILP có thể
trở nên khó khăn với số lượng LLMs rất lớn. Ngoài ra, phương pháp adaptive sampling dựa trên Bayes Factor
có thể cần điều chỉnh cho các loại nhiệm vụ khác nhau. Hướng phát triển tương lai bao gồm việc mở rộng
phương pháp cho các nhiệm vụ multimodal và khám phá các cách tiếp cận hiệu quả hơn cho việc tối ưu hóa ensemble.
🔧 Chi Tiết Kỹ Thuật
📈 Datasets Sử Dụng
- AIME2024: American Invitational Mathematics Examination – 15 bài toán toán học khó
- AIME2025: Phiên bản mới của AIME với độ khó tương tự
- GPQA-DIAMOND: Graduate-level Physics Questions – 448 câu hỏi vật lý trình độ sau đại học
- MATH500: Mathematical reasoning problems – 500 bài toán toán học từ MATH dataset
🤖 LLMs Được Test
- GPT-OSS-20B (OpenAI) – 20B parameters
- Phi-4-reasoning (Microsoft) – 14B parameters
- Qwen3-30B-A3B-Thinking – 30B parameters
- Nemotron-Nano-9B-v2 (NVIDIA) – 9B parameters
- EXAONE-Deep-32B – 32B parameters
- MetaStone-S1-32B – 32B parameters
- Và 5 mô hình khác
💻 Source Code và Dataset
Source code của nghiên cứu này có sẵn tại:
https://github.com/jkomiyama/BoInf-code-publish
Dataset với hơn 3,500 thế hệ cho mỗi kết hợp LLM–dataset sẽ được phát hành để thúc đẩy nghiên cứu tiếp theo
trong lĩnh vực test-time computation và LLM ensemble.
⚙️ Hyperparameters và Cài Đặt
- Concentration parameter α: 0.3 cho tất cả thí nghiệm
- Bayes factor threshold B: Được điều chỉnh cho từng dataset
- Maximum samples N_max: 100 cho adaptive sampling
- Monte Carlo samples: 1,000 cho tính toán Bayes factor
- Independent runs: 100 cho mỗi thí nghiệm
